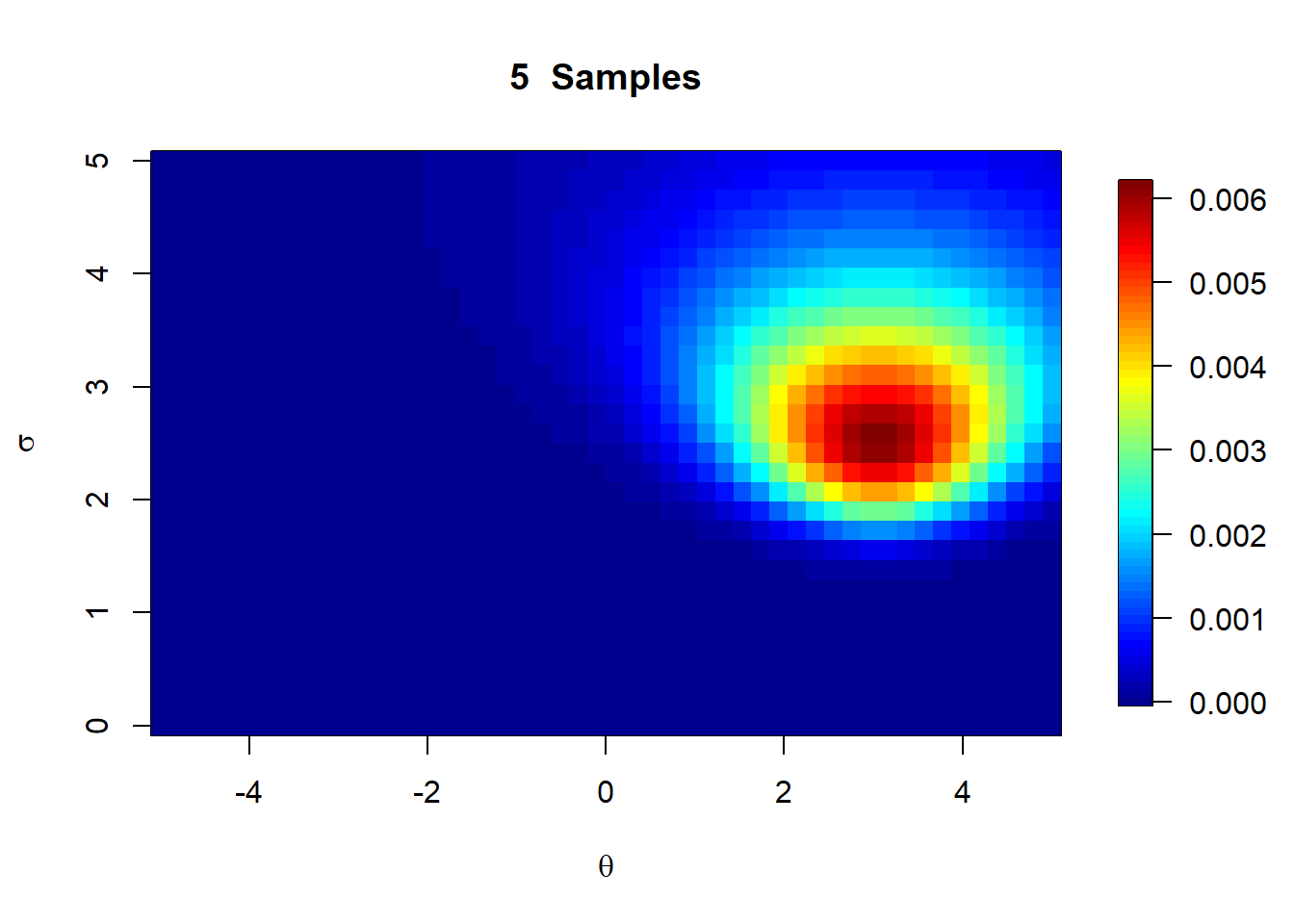
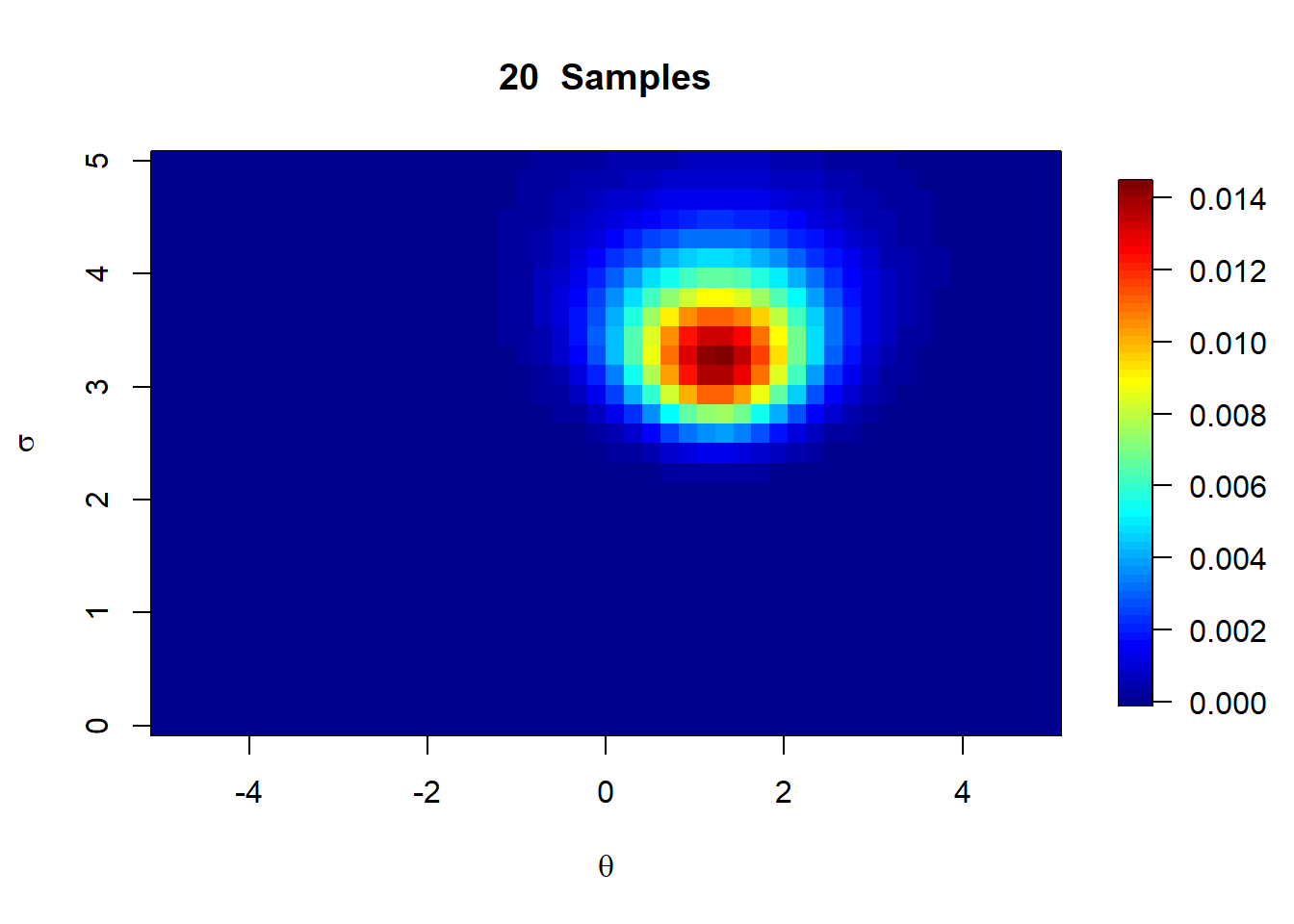
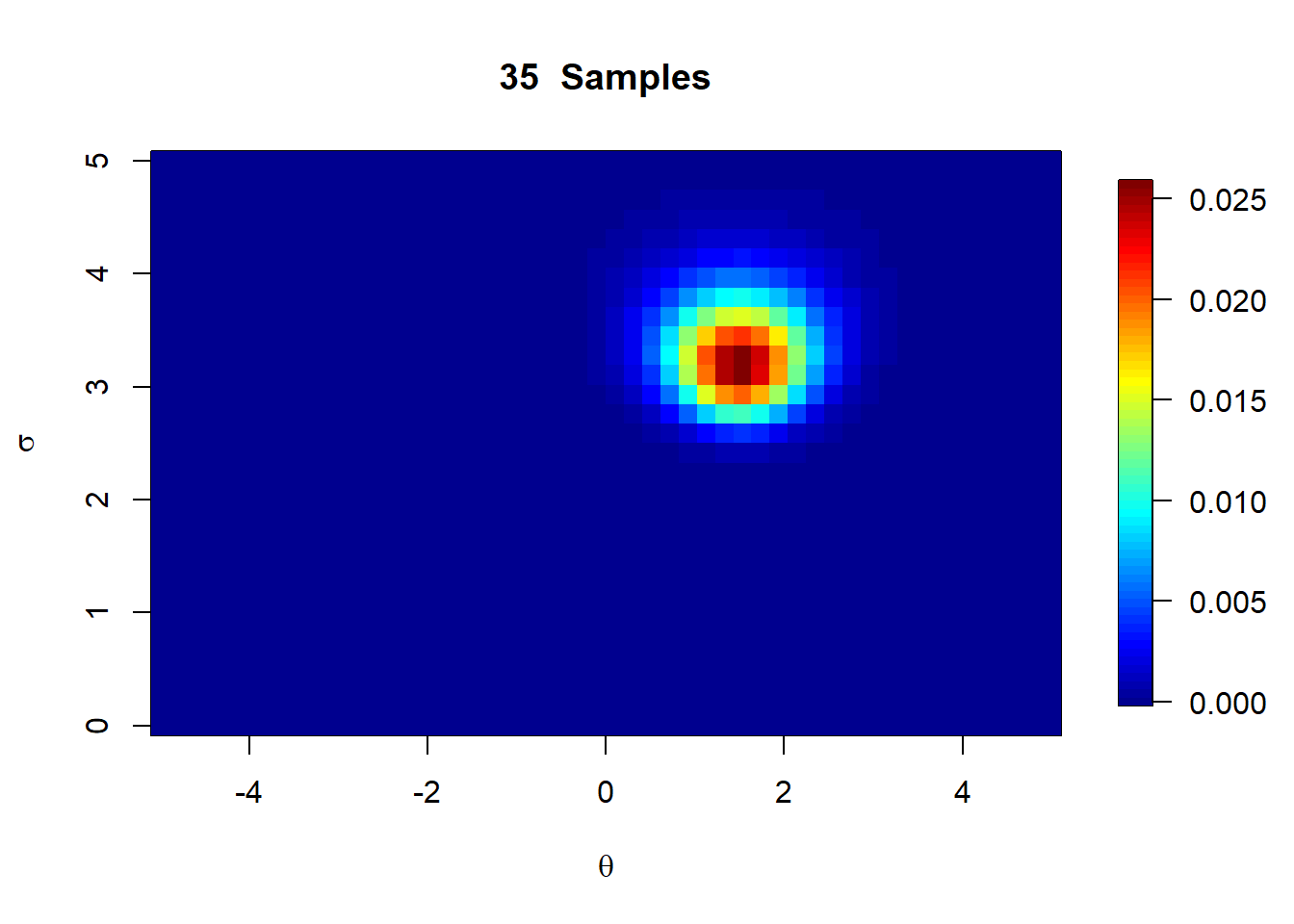
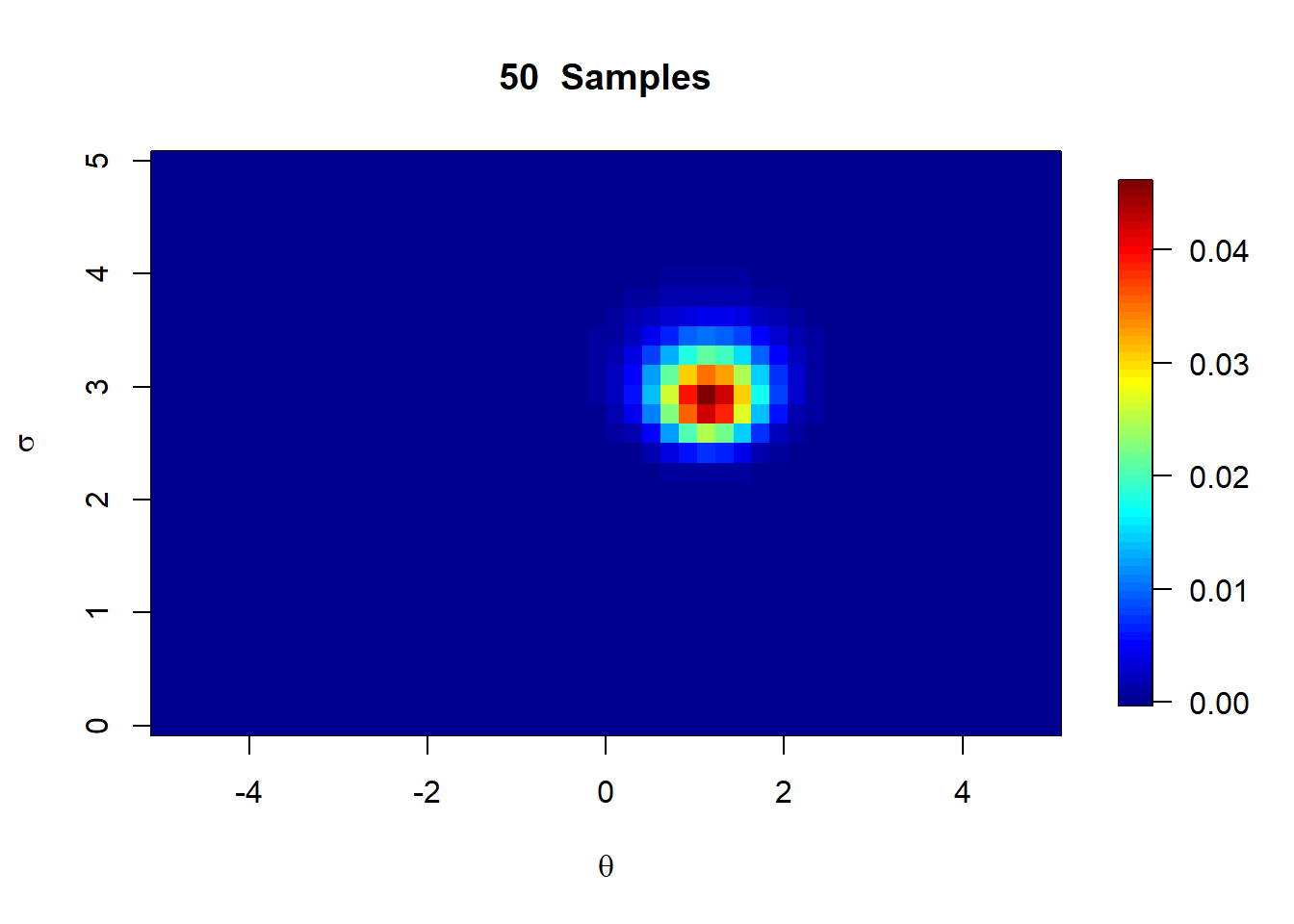
The normal distribution is a great example of a situation where a marginalized posterior may be of interest. In many cases, we may see the variance parameter in the normal distribution as a nuisance parameter, and may only be interested in the posterior distribution for the mean. We can therefore use it as a practical way of learning how to derive a marginal posterior.
We can start with a simpler setting where the variance is assumed to be known. We did something similar in a (________________) previous chapter where the mean was known and the variance unknown. These models provide a simple approach for deriving the conditional posteriors in cases where neither parameter is known.
One observation
In a setting with one observation \(Y\) coming from a normal distribution with known variance \(\sigma_0^2 > 0\) and unknown mean \(\theta\). The conjugate prior in this setting is another normal:
\[
Y \sim Normal(\theta,\sigma_0^2) \\
\theta \sim Normal(\mu_0,\tau_0^2)
\]
With this formulation we have the following likelihood and prior pdfs:
\[
p(y|\theta) = \frac{1}{\sqrt{2\pi\sigma_0^2}} \exp\left(-\frac{(y - \theta)^2}{2\sigma_0^2}\right) \propto \exp\left(-\frac{(y - \theta)^2}{2\sigma_0^2}\right) \\
\]
\[
p(\theta) = \frac{1}{\sqrt{2\pi\tau_0^2}} \exp\left(-\frac{(\theta - \mu_0)^2}{2\tau_0^2}\right) \propto \exp\left(-\frac{(\theta - \mu_0)^2}{2\tau_0^2}\right)
\]
with the unnormalized posterior being:
\[
p(\theta|y)\propto \exp\left(-\frac{(y - \theta)^2}{2\sigma_0^2}-\frac{(\theta - \mu_0)^2}{2\tau_0^2} \right) \\
\propto \exp\left(-\frac{\tau_0^2(y - \theta)^2 + \sigma_0^2(\theta - \mu_0)^2}{2\tau_0^2\sigma_0^2}\right) \\
\propto \exp\left(\frac{\tau_0^2(\theta^2-2y\theta) + \sigma_0^2(\theta^2 -2\mu_0\theta)}{2\tau_0^2\sigma_0^2}\right) \\
\propto \exp\left(-\frac{(\sigma_0^2 + \tau_0^2)\theta^2 -2(\sigma_0^2\mu_0 + \tau_0^2y)\theta}{2\tau_0^2\sigma_0^2}\right) \\
\propto \exp\left(-\frac{\theta^2 -2\mu_1\theta}{2\tau_1^2}\right)
\]
Where
\[
\mu_1 = \frac{(\sigma_0^2\mu_0 + \tau_0^2y)}{(\sigma_0^2 + \tau_0^2)} \\
\tau_1 = \frac{\tau_0^2\sigma_0^2}{(\sigma_0^2 + \tau_0^2)}
\]
Which returns a posterior in the form of a normal distribution with mean \(\mu_1\) and variance \(\tau_1^2\). It is also possible to write the parameters of the posterior in terms of precision. Precision is the inverse of the posterior variance, and can be expressed as the sum of the prior and sampling precision.
\[
\frac{1}{\tau_1^2} = \frac{1}{\tau_0^2} + \frac{1}{\sigma_0^2}
\]
Similarly, the posterior mean can be expressed as a convex combination (sum of prior and sampling means weighted by the proportion of their proportional precision) of the prior mean and the observed data.
\[
\mu_1 = \frac{\frac{1}{\tau_0^2}\mu_0 + \frac{1}{\sigma_0^2}y}{\frac{1}{\tau_0^2} + \frac{1}{\sigma_0^2}}
\]
Many observations
Making the derivation for multiple observations works in a similar fashion, except that we now use a joint-likelihood:
\[
p(y|\theta) = \prod_{i = 1}^np(y_i|\theta)
\]
To make the calculation simple, we can take advantage of the fact that the mean of the normally distributed variables follows a normal distribution too:
\[
\overline{Y} \sim Normal(\theta,\sigma^2/n)
\]
We can then use the solution for the single observation example (and now you see why we started with that :) ) to derive the posterior parameters as:
\[
\mu_n = \frac{\frac{1}{\tau_0^2}\mu_0 + \frac{n}{\sigma_0^2}\overline{y}}{\frac{1}{\tau_0^2} + \frac{n}{\sigma_0^2}}
\]
and
\[
\frac{1}{\tau_n^2} = \frac{1}{\tau_0^2} + \frac{n}{\sigma_0^2}
\]
Now if we had not derive the single observation posterior first, we could have also done this the hard way. But since you’re already here, I say why not both?
We start with expanding the joint likelihood:
\[
p(y|\theta) = \prod_{i = 1}^np(y_i|\theta) = \left(\frac{1}{\sqrt{2\pi\sigma^2}}\right)^n\exp\left(\frac{\sum_{i=1}^n(y_i - \theta)^2}{2\sigma^2}\right)
\]
\[
\propto \exp\left(-\frac{\sum_{i=1}^n(y_i - \theta)^2}{2\sigma^2}\right)
\]
At first glance it may look daunting to find a closed form solution to our problem and identifying a sufficient statistic seems unlikely. However, we can rely on the achievements of our predecessors to get through this. Here, we can use sum of squares decomposition:
\[\sum_{i=1}^n(y_i - \theta)^2 = n(\overline{y} - \theta)^2 + \sum_{i=1}^n(y_i - \overline{y})^2\]
Where \(\overline{y}\) is the mean of the observed values. We now have the following:
\[
p(y|\theta)\propto \exp\left(-\frac{n(\overline{y} - \theta)^2 + \sum_{i=1}^n(y_i - \overline{y})^2}{2\sigma^2}\right)
\]
\[
\propto \exp\left(-\frac{n(\overline{y} - \theta)^2}{2\sigma^2}\right)
\]
As the second component does not depend on \(\theta\). All of a sudden we now have a pdf that depends only on a sufficient statistic! We can now multiply this by the prior and see that it matches the form of the posterior we saw earlier:
\[
p(\theta|y) \propto \exp\left(\frac{n(\overline{y} - \theta)^2}{2\sigma^2}\right)\exp\left(-\frac{(\theta - \mu_0)^2}{2\tau_0^2}\right)
\]
\[
= \exp\left(-\frac{n\tau_0^2(\overline{y} - \theta)^2 + \sigma_0^2(\theta - \mu_0)^2}{2\tau_0^2\sigma_0^2}\right)
\]
From here we can notice the similar form of the posterior from the single observation example, with the only exception being that there is also the variable \(n\).